Batch 2 - Class 287 - Compositions
Zoom: send meeting Id and password
Start recording
Preclass Exercise:
- Find the winning strategy for the following game. There are 15 coins in a row. Each player can pick 1, 2 or 3 adjacent coins in her turn. Note that two coins from between which a coins has been removed do not count as adjacent. Then the next player does the same, and so on. Person who picks the last coin(s) wins. Does the first player have a winning strategy? If so, what is it?
- Answer: Pick the middle coin to leave two rows of 7 coins each. Now replicate whatever move the opponent makes to preserve symmetry after every more.
Attendance: Raghav, Kabir, Shikhar, Ayush, Rhea Chadha, Ryan Chadha, Rohan, Yatharth, Anika, Vansh, Adyant, Ekagra, Mihir, Advay, Aneesh, Siddharth, Tarush, Vivaan, Nikhil Pande
Class Notes: (repeat from class 78)
There are four ways for 3 to be the total of a list of positive integers:
3 = 2 + 1 = 1 + 2 = 1 + 1 + 1.
Some people prefer to write the same thing with tally marks instead of numbers:
| | | = | |+| = |+| | = |+|+|.
We say there are four compositions of 3. The numbers making up each composition are called the parts, so for example one of the compositions of 3 has first part 2 and second part 1. We'll find some patterns by organizing these lists of compositions in different ways.
- List all the compositions of 1. Now try 2. Now try 3 (which you can just copy from the introduction up there!). Now try 4. How many compositions does it have?
- Do you see a pattern here? Can you see why the pattern will continue that way? How many compositions will 10 have?
- Answer: These are powers of 2. Why? Note that you can take each of the partition points, and either place a "+" there or not. Each such choice gives a different composition.
- Now we're going to organize our compositions by the size of the first part. For 3, we see that two of the compositions begin with 1, one composition begins with 2, and one with 3. Can you finish filling in the chart below? What patterns do you notice? Why do they occur?
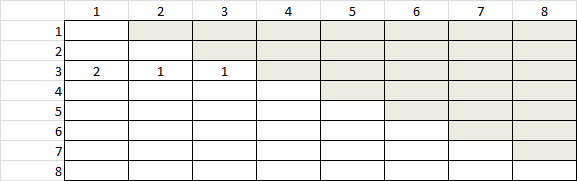
- Answer:
- If you look at all the compositions of a number, how many of them are made of only odd parts? For instance, some of the compositions of 5 that would work are 5, 1 + 3 + 1, and 1 + 1 + 1 + 1 + 1, but there are others. How many?
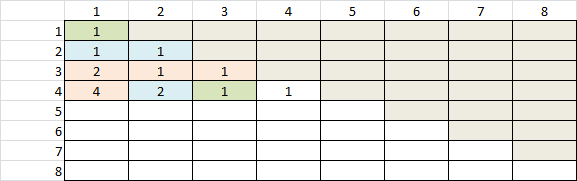
- Organize your compositions by the number of parts. In other words, for 3 we'd list that there is one composition with 1 part, two with 2 parts, and one with 3 parts. Do the same thing for the compositions of several other numbers, and hunt for patterns. Can you predict how many compositions of 8 have exactly 5 parts?
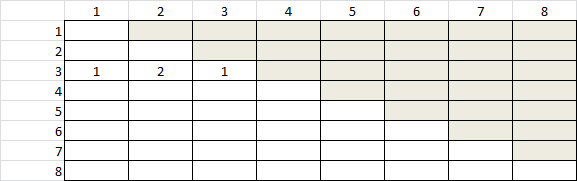
- Answer: Its nC0, nC1, nC2 and so on - Why?
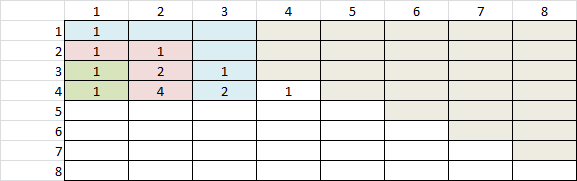
- Organize your compositions by the size of the largest part. For 3, we'd have one composition whose largest part is 3, two whose largest part is 2, and one whose largest part is 1. What patterns can you uncover now? Can you predict how many compositions of 8 have 3 as their largest part?

- Answer: Can you think of it as choosing a first partition, and then applying recursion on previous choices?
Homework
- What If? Can you use a magnifying glass and moonlight to light a fire?
- Sun is about 400,000 times brighter than Moon. One can use a lens to concentrate light of sun and light a fire. Can you use a much larger lens and light a fire using moonlight?
References: